Competitive inhibition
Competitive inhibition is a form of enzyme inhibition where binding of the inhibitor to the active site on the enzyme prevents binding of the substrate and vice versa.
Contents |
Mechanism
In competitive inhibition, at any given moment, the enzyme may be bound to the inhibitor, the substrate, or neither, but it cannot bind both at the same time.
In virtually every case, competitive inhibitors bind in the same binding site as the substrate, but same-site binding is not a requirement. A competitive inhibitor could bind to an allosteric site of the free enzyme and prevent substrate binding, as long as does not bind to the allosteric site when the substrate is bound.
In competitive inhibition, the maximum velocity (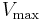 ) of the reaction is unchanged, while the apparent affinity of the substrate to the binding site is decreased (the
) of the reaction is unchanged, while the apparent affinity of the substrate to the binding site is decreased (the 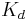 dissociation constant is apparently increased). The change in
dissociation constant is apparently increased). The change in 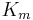 (Michaelis-Menten constant) is parallel to the alteration in
(Michaelis-Menten constant) is parallel to the alteration in 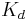 . Any given competitive inhibitor concentration can be overcome by increasing the substrate concentration in which case the substrate will outcompete the inhibitor in binding to the enzyme.
. Any given competitive inhibitor concentration can be overcome by increasing the substrate concentration in which case the substrate will outcompete the inhibitor in binding to the enzyme.
Equation
Competitive inhibition increases the apparent value of the Michaelis-Menten constant, 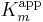 , such that initial rate of reaction,
, such that initial rate of reaction, 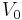 , is given by
, is given by
where ![K^\text{app}_m=K_m(1%2B[I]/K_i)](/2012-wikipedia_en_all_nopic_01_2012/I/ae638c0a7d6dd266baeaf2fe7eb81c5c.png) ,
, 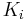 is the inhibitor's dissociation constant and
is the inhibitor's dissociation constant and ![[I]](/2012-wikipedia_en_all_nopic_01_2012/I/cc3bb9e406ac145fe2786bf9e88523cf.png) is the inhibitor concentration.
is the inhibitor concentration.
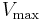 remains the same because the presence of the inhibitor can be overcome by higher substrate concentrations.
remains the same because the presence of the inhibitor can be overcome by higher substrate concentrations. 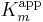 , the substrate concentration that is needed to reach
, the substrate concentration that is needed to reach 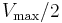 , increases with the presence of a competitive inhibitor. This is because the concentration of substrate needed to reach
, increases with the presence of a competitive inhibitor. This is because the concentration of substrate needed to reach 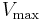 with an inhibitor is greater than the concentration of substrate needed to reach
with an inhibitor is greater than the concentration of substrate needed to reach 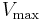 without an inhibitor.
without an inhibitor.
Derivation
In the simplest case of a single-substrate enzyme obeying Michaelis-Menten kinetics, the typical scheme
is modified to include binding of the inhibitor to the free enzyme:
Note that the inhibitor does not bind to the ES complex and the substrate does not bind to the EI complex. It is generally assumed that this behavior is indicative of both compounds binding at the same site, but that is not strictly necessary. As with the derivation of the Michaelis-Menten equation, assume that the system is at steady-state, i.e. the concentration of each of the enzyme species is not changing.
Furthermore, the known total enzyme concentration is ![[E]_0 = [E] %2B [ES] %2B [EI]](/2012-wikipedia_en_all_nopic_01_2012/I/f1b9bd1a10c25790194821c07757c407.png) , and the velocity is measured under conditions in which the substrate and inhibitor concentrations do not change substantially and an insignificant amount of product has accumulated.
, and the velocity is measured under conditions in which the substrate and inhibitor concentrations do not change substantially and an insignificant amount of product has accumulated.
We can therefore set up a system of equations:
-
![[E]_0 = [E] %2B [ES] %2B [EI]\,\!](/2012-wikipedia_en_all_nopic_01_2012/I/9333f81d3469225c43ca5ab45c11c3f9.png)
(
-
![\frac{d[E]}{dt} = 0 = -k_1[E][S] %2B k_{-1}[ES] %2B k_2[ES] -k_3[E][I] %2B k_{-3}[EI]](/2012-wikipedia_en_all_nopic_01_2012/I/0b83633fb5fa8024a826d0bcc1c0897e.png)
(
-
![\frac{d[ES]}{dt} = 0 = k_1[E][S] - k_{-1}[ES] - k_2[ES]](/2012-wikipedia_en_all_nopic_01_2012/I/00e9f52d6c0736059680a4711745f0eb.png)
(
-
![\frac{d[EI]}{dt} = 0 = k_3[E][I] - k_{-3}[EI]](/2012-wikipedia_en_all_nopic_01_2012/I/a60c034eca4b94a2e6ed79a9de58d09d.png)
(
where ![[S]](/2012-wikipedia_en_all_nopic_01_2012/I/38bd6c19740e43396bd14b1575d58f60.png) ,
, ![[I]](/2012-wikipedia_en_all_nopic_01_2012/I/cc3bb9e406ac145fe2786bf9e88523cf.png) and
and ![[E]_0](/2012-wikipedia_en_all_nopic_01_2012/I/357bc494f724ede952492cec26d55c2a.png) are known. The initial velocity is defined as
are known. The initial velocity is defined as ![V_0 = d[P]/dt = k_2 [ES]](/2012-wikipedia_en_all_nopic_01_2012/I/69e38ea7fd6007bd2d5173f512372b6e.png) , so we need to define the unknown
, so we need to define the unknown ![[ES]](/2012-wikipedia_en_all_nopic_01_2012/I/b1ddeae984d7c294737d9b66480377ea.png) in terms of the knowns
in terms of the knowns ![[S]](/2012-wikipedia_en_all_nopic_01_2012/I/38bd6c19740e43396bd14b1575d58f60.png) ,
, ![[I]](/2012-wikipedia_en_all_nopic_01_2012/I/cc3bb9e406ac145fe2786bf9e88523cf.png) and
and ![[E]_0](/2012-wikipedia_en_all_nopic_01_2012/I/357bc494f724ede952492cec26d55c2a.png) .
.
From equation (3), we can define E in terms of ES by rearranging to
Dividing by ![k_1[S]](/2012-wikipedia_en_all_nopic_01_2012/I/85654d6205e3dab04816f1716949f999.png) gives
gives
As in the derivation of the Michaelis-Menten equation, the term 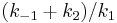 can be replaced by the macroscopic rate constant
can be replaced by the macroscopic rate constant 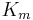 :
:
-
![[E] = \frac{K_m[ES]}{[S]}](/2012-wikipedia_en_all_nopic_01_2012/I/a25186256c8ed06fcb4c089797487844.png)
(
Substituting equation (5) into equation (4), we have
Rearranging, we find that
At this point, we can define the dissociation constant for the inhibitor as 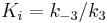 , giving
, giving
-
![[EI] = \frac{K_m[I][ES]}{K_i[S]}](/2012-wikipedia_en_all_nopic_01_2012/I/118c106b2b4dbf6f779d740269f9445f.png)
(
At this point, substitute equation (5) and equation (6) into equation (1):
Rearranging to solve for ES, we find
-
![[ES] = \frac{K_i [S][E]_0}{K_m K_i %2B K_i[S] %2B K_m[I]}](/2012-wikipedia_en_all_nopic_01_2012/I/b83afab74a37b3a1a114c6d33a361ada.png)
(
Returning to our expression for 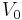 , we now have:
, we now have:
![\begin{align}
V_0 & = k_2[ES] = \frac{k_2 K_i [S][E]_0}{K_m K_i %2B K_i[S] %2B K_m[I]} \\
& = \frac{k_2 [E]_0 [S]}{K_m %2B [S] %2B K_m\frac{[I]}{K_i}}
\end{align}](/2012-wikipedia_en_all_nopic_01_2012/I/1e987b87a78842a9bc9ac9dcf108c499.png)
Since the velocity is maximal when all the enzyme is bound as the enzyme-substrate complex, ![V_\max = k_2 [E]_0](/2012-wikipedia_en_all_nopic_01_2012/I/c23a2971a66027ff14a23ff7cf17e972.png) . Replacing and combining terms finally yields the conventional form:
. Replacing and combining terms finally yields the conventional form:
-
![V_0 = \frac{V_\max[S]}{K_m(1 %2B \frac{[I]}{K_i}) %2B [S]}](/2012-wikipedia_en_all_nopic_01_2012/I/5cabee32477d64dbf6bf4988abdd0df0.png)
(
See also
- Schild regression for ligand receptor inhibition
|
|||||||||||||||||||
![V_0 = \frac{V_\max[S]}{K^\text{app}_m %2B [S]}](/2012-wikipedia_en_all_nopic_01_2012/I/f0eec6bef5579284a6810b2c76130f24.png)
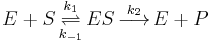
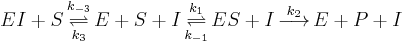
![\frac{d[E]}{dt} = \frac{d[ES]}{dt} = \frac{d[EI]}{dt} = 0.](/2012-wikipedia_en_all_nopic_01_2012/I/8d01b36062626fb97e6fcec58d399beb.png)
![k_1[E][S]=(k_{-1}%2Bk_2)[ES] \,\!](/2012-wikipedia_en_all_nopic_01_2012/I/247e77fcb03bcc569e4f34428efc385d.png)
![[E] = \frac{(k_{-1}%2Bk_2)[ES]}{k_1[S]}](/2012-wikipedia_en_all_nopic_01_2012/I/7a8a4ae33a0c42b7af38d62bcfcb1eca.png)
![0 = \frac{k_3[I]K_m[ES]}{[S]} - k_{-3}[EI]](/2012-wikipedia_en_all_nopic_01_2012/I/eb6c67789f07fae44bb9573b0e83c6d9.png)
![[EI] = \frac{K_m k_3[I][ES]}{k_{-3}[S]}](/2012-wikipedia_en_all_nopic_01_2012/I/5a4027848952a0e51403bcff88ac77a8.png)
![[E]_0 = \frac{K_m[ES]}{[S]} %2B [ES] %2B \frac{K_m[I][ES]}{K_i[S]}](/2012-wikipedia_en_all_nopic_01_2012/I/fa1f6e643e6006c7aedd86543d640d1e.png)
![[E]_0 = [ES] \left ( \frac{K_m}{[S]} %2B 1 %2B \frac{K_m[I]}{K_i[S]} \right )= [ES] \frac{K_m K_i %2B K_i[S] %2B K_m[I]}{K_i[S]}](/2012-wikipedia_en_all_nopic_01_2012/I/36de9f2af9d3bfa7ec037909b5762e31.png)